17 KiB
决策树-ID3 算法
决策树的基本认识
决策树是一种依托决策而建立起来的一种树。在机器学习中,决策树是一种预测模型,代表的是一种对象属性与对象值之间的一种映射关系,每一个节点代表某个对象,树中的每一个分叉路径代表某个可能的属性值,而每一个叶子节点则对应从根节点到该叶子节点所经历的路径所表示的对象的值。决策树仅有单一输出,如果有多个输出,可以分别建立独立的决策树以处理不同的输出。接下来讲解ID3算法。
ID3算法介绍
ID3算法是决策树的一种,它是基于奥卡姆剃刀原理的,即用尽量用较少的东西做更多的事。ID3算法,即Iterative Dichotomiser 3,迭代二叉树3代,是Ross Quinlan发明的一种决策树算法,这个算法的基础就是上面提到的奥卡姆剃刀原理,越是小型的决策树越优于大的决策树,尽管如此,也不总是生成最小的树型结构,而是一个启发式算法。
在信息论中,期望信息越小,那么信息增益就越大,从而纯度就越高。ID3算法的核心思想就是以信息增益来度量属性的选择,选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍历可能的决策空间。
信息熵与信息增益
在信息增益中,重要性的衡量标准就是看特征能够为分类系统带来多少信息,带来的信息越多,该特征越重要。在认识信息增益之前,先来看看信息熵的定义
熵这个概念最早起源于物理学,在物理学中是用来度量一个热力学系统的无序程度,而在信息学里面,熵是对不确定性的度量。在1948年,香农引入了信息熵,将其定义为离散随机事件出现的概率,一个系统越是有序,信息熵就越低,反之一个系统越是混乱,它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。
假如一个随机变量 X 的取值为 X={x1,x2,...xn},每一种取到的概率分别是 {p1,p2,...,pn},那么 X 的熵定义为
H(X) = -sum(i=1, n, pi*log2(pi))
意思是一个变量的变化情况可能越多,那么它携带的信息量就越大。
对于分类系统来说,类别 C 是变量,它的取值是 C1,C2,...,Cn,而每一个类别出现的概率分别是
P(C1),P(C2),...,P(Cn)
而这里的 n 就是类别的总数,此时分类系统的熵就可以表示为
H(C) = -sum(i=1, n, P(Ci)*log2(P(Ci)))
以上就是信息熵的定义,接下来介绍信息增益。
信息增益是针对一个一个特征而言的,就是看一个特征 t ,系统有它和没有它时的信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即信息增益。
接下来以天气预报的例子来说明。下面是描述天气数据表,学习目标是 play 或者 not play。
| Outlook | Temperature | Humidity | Windy | Play? |
|---|---|---|---|---|
| sunny | hot | high | false | no |
| sunny | hot | high | true | no |
| overcast | hot | high | false | yes |
| rain | mild | high | false | yes |
| rain | cool | normal | false | yes |
| rain | cool | normal | true | no |
| overcast | cool | normal | true | yes |
| sunny | mild | high | false | no |
| sunny | cool | normal | false | yes |
| rain | mild | normal | false | yes |
| sunny | mild | normal | true | yes |
| overcast | mild | high | true | yes |
| overcast | hot | normal | false | yes |
| rain | mild | high | true | no |
可以看出,一共14个样例,包括9个正例和5个负例。那么当前信息的熵计算如下
Entropy(S) = -9/14*log2(9/14)-5/14*log2(5/14) = 0.940286
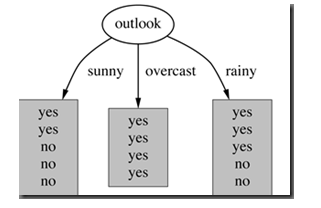
在决策树分类问题中,信息增益就是决策树在进行属性选择划分前和划分后信息的差值。假设利用属性 Outlook 来分类,那么如下图
划分后,数据被分为三部分了,那么各个分支的信息熵计算如下
Entropy(sunny) = -2/5*log2(2/5)-3/5*log2(3/5) = 0.970951
Entropy(overcast) = -4/4*log2(4/4)-0*log2(0) = 0
Entropy(rainy) = -3/5*log2(3/5)-2/5*log2(2/5) = 0.970951
那么划分后的信息熵为
Entropy(S|T) = 5/14*0.970951+4/14*0+5/14*0.970951 = 0.693536
Entropy(S|T) 代表在特征属性 T 的条件下样本的条件熵。那么最终得到特征属性 T 带来的信息增益为
IG(T) = Entropy(S)-Entropy(S|T) = 0.24675
信息增益的计算公式如下
IG(S|T) = Entropy(S)-sum(value(T), , |Sv|/S*Entropy(Sv))
其中 S 全部样本集合,value(T) 是属性 T 所有取值的集合,v 是 T 的其中一个属性值,Sv 是 S 中属性 T 的值为 v 的样例集合,|Sv| 为 Sv 中所含样例数。
在决策树的每一个非叶子结点划分之前,先计算每一个属性所带来的信息增益,选择最大信息增益的属性来划分,因为信息增益越大,区分样本的能力就越强,越具有代表性,很显然这是一种自顶向下的贪心策略。以上就是ID3算法的核心思想。
决策树停止的条件
如果发生以下的情况,决策树将停止分割
- 改群数据的每一笔数据已经归类到每一类数据中,即数据已经不能继续在分。
- 该群数据已经找不到新的属性进行节点分割
- 该群数据没有任何未处理的数据
ID3 算法的 C++ 实现
接下来开始用 C++ 实现 ID3 算法,包括以下文件
ID3.cpp ID3.h main.cpp Makefile Test
/**
* @file ID3.h
*/
#ifndef _ID3_H_
#define _ID3_H_
#include <utility>
#include <list>
#include <map>
#define Type int //样本数据类型
#define Map1 std::map< int, Type > //定义一维map
#define Map2 std::map< int, Map1 > //定义二维map
#define Map3 std::map< int, Map2 > //定义三维map
#define Pair std::pair<int, Type>
#define List std::list< Pair > //一维list
#define SampleSpace std::list< List > //二维list 用于存放样本数据
#define Child std::map< int, Node* > //定义后继节点集合
#define CI const_iterator
/*
* 在ID3算法中,用二维链表存放样本,结构为list< list< pair<int, int> > >,简记为SampleSpace,取名样本空间
* 样本数据从根节点开始往下遍历。每一个节点的定义如下结构体
*/
struct Node
{
int index; //当前节点样本最大增益对应第index个属性,根据这个进行分类的
int type; //当前节点的类型
Child next; //当前节点的后继节点集合
SampleSpace sample; //未分类的样本集合
};
class ID3{
public:
ID3(int );
~ID3();
void PushData(const Type*, const Type); //将样本数据Push给二维链表
void Build(); //构建决策树
int Match(const Type*); //根据新的样本预测结果
void Print(); //打印决策树的节点的值
private:
void _clear(Node*);
void _build(Node*, int);
int _match(const int*, Node*);
void _work(Node*);
double _entropy(const Map1&, double);
int _get_max_gain(const SampleSpace&);
void _split(Node*, int);
void _get_data(const SampleSpace&, Map1&, Map2&, Map3&);
double _info_gain(Map1&, Map2&, double, double);
int _same_class(const SampleSpace&);
void _print(Node*);
private:
int dimension;
Node *root;
};
#endif // _ID3_H_
/**
* @file ID3.cpp
*/
#include <iostream>
#include <cassert>
#include <cmath>
#include "ID3.h"
using namespace std;
//初始化ID3的数据成员
ID3::ID3(int dimension)
{
this->dimension = dimension;
root = new Node();
root->index = -1;
root->type = -1;
root->next.clear();
root->sample.clear();
}
//清空整个决策树
ID3::~ID3()
{
this->dimension = 0;
_clear(root);
}
//x为dimension维的属性向量,y为向量x对应的值
void ID3::PushData(const Type *x, const Type y)
{
List single;
single.clear();
for(int i = 0; i < dimension; i++)
single.push_back(make_pair(i + 1, x[i]));
single.push_back(make_pair(0, y));
root->sample.push_back(single);
}
void ID3::_clear(Node *node)
{
Child &next = node->next;
Child::iterator it;
for(it = next.begin(); it != next.end(); it++)
_clear(it->second);
next.clear();
delete node;
}
void ID3::Build()
{
_build(root, dimension);
}
void ID3::_build(Node *node, int dimension)
{
//获取当前节点未分类的样本数据
SampleSpace &sample = node->sample;
//判断当前所有样本是否是同一类,如果不是则返回-1
int y = _same_class(sample);
//如果所有样本是属于同一类
if(y >= 0)
{
node->index = -1;
node->type = y;
return;
}
//在_max_gain()函数中计算出当前节点的最大增益对应的属性,并根据这个属性对数据进行划分
_work(node);
//Split完成后清空当前节点的所有数据,以免占用太多内存
sample.clear();
Child &next = node->next;
for(Child::iterator it = next.begin(); it != next.end(); it++)
_build(it->second, dimension - 1);
}
//判断当前所有样本是否是同一类,如果不是则返回-1
int ID3::_same_class(const SampleSpace &ss)
{
//取出当前样本数据的一个Sample
const List &f = ss.front();
//如果没有x属性,而只有y,直接返回y
if(f.size() == 1)
return f.front().second;
Type y = 0;
//取出第一个样本数据y的结果值
for(List::CI it = f.begin(); it != f.end(); it++)
{
if(!it->first)
{
y = it->second;
break;
}
}
//接下来进行判断,因为list是有序的,所以从前往后遍历,发现有一对不一样,则所有样本不是同一类
for(SampleSpace::CI it = ss.begin(); it != ss.end(); it++)
{
const List &single = *it;
for(List::CI i = single.begin(); i != single.end(); i++)
{
if(!i->first)
{
if(y != i->second)
return -1; //发现不是同一类则返回-1
else
break;
}
}
}
return y; //比较完所有样本的输出值y后,发现是同一类,返回y值。
}
void ID3::_work(Node *node)
{
int mai = _get_max_gain(node->sample);
assert(mai >= 0);
node->index = mai;
_split(node, mai);
}
//获取最大的信息增益对应的属性
int ID3::_get_max_gain(const SampleSpace &ss)
{
Map1 y;
Map2 x;
Map3 xy;
_get_data(ss, y, x, xy);
double s = ss.size();
double entropy = _entropy(y, s); //计算熵值
int mai = -1;
double mag = -1;
for(Map2::iterator it = x.begin(); it != x.end(); it++)
{
double g = _info_gain(it->second, xy[it->first], s, entropy); //计算信息增益值
if(g > mag)
{
mag = g;
mai = it->first;
}
}
if(!x.size() && !xy.size() && y.size()) //如果只有y数据
return 0;
return mai;
}
//获取数据,提取出所有样本的y值,x[]属性值,以及属性值和结果值xy。
void ID3::_get_data(const SampleSpace &ss, Map1 &y, Map2 &x, Map3 &xy)
{
for(SampleSpace::CI it = ss.begin(); it != ss.end(); it++)
{
int c = 0;
const List &v = *it;
for(List::CI p = v.begin(); p != v.end(); p++)
{
if(!p->first)
{
c = p->second;
break;
}
}
++y[c];
for(List::CI p = v.begin(); p != v.end(); p++)
{
if(p->first)
{
++x[p->first][p->second];
++xy[p->first][p->second][c];
}
}
}
}
//计算熵值
double ID3::_entropy(const Map1 &x, double s)
{
double ans = 0;
for(Map1::CI it = x.begin(); it != x.end(); it++)
{
double t = it->second / s;
ans += t * log2(t);
}
return -ans;
}
//计算信息增益
double ID3::_info_gain(Map1 &att_val, Map2 &val_cls, double s, double entropy)
{
double gain = entropy;
for(Map1::CI it = att_val.begin(); it != att_val.end(); it++)
{
double r = it->second / s;
double e = _entropy(val_cls[it->first], it->second);
gain -= r * e;
}
return gain;
}
//对当前节点的sample进行划分
void ID3::_split(Node *node, int idx)
{
Child &next = node->next;
SampleSpace &sample = node->sample;
for(SampleSpace::iterator it = sample.begin(); it != sample.end(); it++)
{
List &v = *it;
for(List::iterator p = v.begin(); p != v.end(); p++)
{
if(p->first == idx)
{
Node *tmp = next[p->second];
if(!tmp)
{
tmp = new Node();
tmp->index = -1;
tmp->type = -1;
next[p->second] = tmp;
}
v.erase(p);
tmp->sample.push_back(v);
break;
}
}
}
}
int ID3::Match(const Type *x)
{
return _match(x, root);
}
int ID3::_match(const Type *v, Node *node)
{
if(node->index < 0)
return node->type;
Child &next = node->next;
Child::iterator p = next.find(v[node->index - 1]);
if(p == next.end())
return -1;
return _match(v, p->second);
}
void ID3::Print()
{
_print(root);
}
void ID3::_print(Node *node)
{
cout << "Index = " << node->index << endl;
cout << "Type = " << node->type << endl;
cout << "NextSize = " << node->next.size() << endl;
cout << endl;
Child &next = node->next;
Child::iterator p;
for(p = next.begin(); p != next.end(); ++p)
_print(p->second);
}
/**
* main.cpp
*/
#include <iostream>
#include "ID3.h"
using namespace std;
enum outlook {SUNNY, OVERCAST, RAIN };
enum temp {HOT, MILD, COOL };
enum hum {HIGH, NORMAL };
enum windy {WEAK, STRONG };
int samples[14][4] =
{
{SUNNY , HOT , HIGH , WEAK },
{SUNNY , HOT , HIGH , STRONG},
{OVERCAST, HOT , HIGH , WEAK },
{RAIN , MILD, HIGH , WEAK },
{RAIN , COOL, NORMAL, WEAK },
{RAIN , COOL, NORMAL, STRONG},
{OVERCAST, COOL, NORMAL, STRONG},
{SUNNY , MILD, HIGH , WEAK },
{SUNNY , COOL, NORMAL, WEAK },
{RAIN , MILD, NORMAL, WEAK },
{SUNNY , MILD, NORMAL, STRONG},
{OVERCAST, MILD, HIGH , STRONG},
{OVERCAST, HOT , NORMAL, WEAK },
{RAIN , MILD, HIGH , STRONG}
};
int main()
{
ID3 Tree(4);
Tree.PushData((int *)&samples[0], 0);
Tree.PushData((int *)&samples[1], 0);
Tree.PushData((int *)&samples[2], 1);
Tree.PushData((int *)&samples[3], 1);
Tree.PushData((int *)&samples[4], 1);
Tree.PushData((int *)&samples[5], 0);
Tree.PushData((int *)&samples[6], 1);
Tree.PushData((int *)&samples[7], 0);
Tree.PushData((int *)&samples[8], 1);
Tree.PushData((int *)&samples[9], 1);
Tree.PushData((int *)&samples[10], 1);
Tree.PushData((int *)&samples[11], 1);
Tree.PushData((int *)&samples[12], 1);
Tree.PushData((int *)&samples[13], 0);
Tree.Build();
Tree.Print();
cout << endl;
for(int i = 0; i < 14; ++i)
cout << "predict value : " <<Tree.Match( (int *)&samples[i] ) << endl;
return 0;
}
# Makefile
Test: main.cpp ID3.h ID3.cpp
g++ -o Test ID3.cpp main.cpp
clean:
rm Test