5.0 KiB
5.0 KiB
| layout | title | subtitle | description | excerpt | date | author | tags | categories | published | math | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| post | 拉格朗日插值 | 给出拉格朗日多项式插值的推导过程和标准公式。 | 通过简单的推导过程和示例程序演示拉格朗日多项式插值。 | 2022-09-08 12:50:00 | Rick Chan |
|
|
true | true |
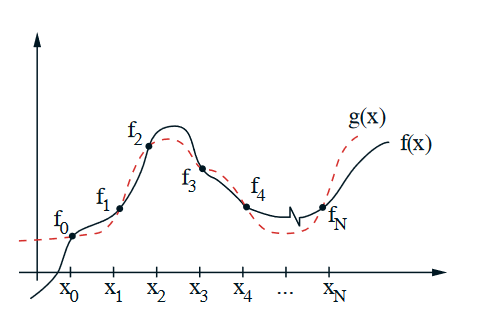
Fit N+1 points with an N^{th} degree polynomial
f(x) = exact function of which only N+1 discrete values are known and used to estab- lish an interpolating or approximating function g(x).
g(x) = approximating or interpolating function. This function will pass through all specified N+1 interpolation points (also referred to as data points or nodes).
The interpolation points or nodes are given as:
\begin{gather*}
x_0 & f(x_0)\equiv f_0 \\
x_1 & f(x_1)\equiv f_1 \\
x_2 & f(x_2)\equiv f_2 \\
... \\
x_N & f(x_N)\equiv f_N
\end{gather*}$$
There exists only one $N^{th}$ degree polynomial that passes through a given set of N+1 points. It’s form is (expressed as a power series):
$$g(x)=a_0+a_1x+a_2x^2+a_3x^3+...+a_Nx^N$$
where $a_i=\text{unknown coefficients}$, $i=0,N\text{(N+1 coefficients)}$.
No matter how we derive the $N^{th}$ degree polynomial:
* Fitting power series
* Lagrange interpolating functions
* Newton forward or backward interpolation
The resulting polynomial will always be the same!
## Power Series Fitting to Define Lagrange Interpolation
g(x) must match f(x) at the selected data points:
$$\begin{gather*}
g(x_0)=f_0 \to a_0+a_1x_0+a_2x_0^2+...+a_Nx_0^N=f_0 \\
g(x_1)=f_1 \to a_0+a_1x_1+a_2x_1^2+...+a_Nx_1^N=f_1 \\
... \\
g(x_N)=f_N \to a_0+a_1x_N+a_2x_N^2+...+a_Nx_N^N=f_N \\
\end{gather*}$$
Solve set of simultaneous equations:
$$\begin{bmatrix}
1 & x_0 & x_0^2 & ... & x_0^N \\
1 & x_1 & x_1^2 & ... & x_1^N \\
... \\
1 & x_N & x_N^2 & ... & x_N^N
\end{bmatrix} \begin{bmatrix}
a_0 \\ a_1 \\ ... \\ a_N
\end{bmatrix} = \begin{bmatrix}
f_0 \\ f_1 \\ ... \\ f_N
\end{bmatrix}$$
It is relatively computationally costly to solve the coefficients of the interpolating function g(x) (i.e. you need to program a solution to these equations).
## Lagrange Interpolation Using Basis Functions
We note that in general:
$$g(x_i)=f_i$$
Let
$$g(x)=\sum_{i=0}^Nf_iV_i(x)$$
where $V_i(x)$ polynomial of degree associated with each node such that
$$\begin{equation*}
V_i(x_j)\equiv \begin{cases}
0 & i\neq j \\
1 & i= j
\end{cases}
\end{equation*}$$
For example if we have 5 interpolation points (or nodes)
$$g(x_3)=f_0V_0(x_3)+f_1V_1(x_3)+f_2V_2(x_3)+f_3V_3(x_3)+f_4V_4(x_3)$$
Using the definition for $V_i(x_j)$:
$$\begin{gather*}
V_0(x_3)=0 \\
V_1(x_3)=0 \\
V_2(x_3)=0 \\
V_3(x_3)=1 \\
V_4(x_4)=0
\end{gather*}$$
we have:
$$g(x_3)=f_3$$
How do we construct $V_i(x)$?
* Degree N
* Roots at $x_0,x_1,x_2,...,x_{i-1},...,x_N$ (at all nodes except $x_i$)
* $V_i(x_i)=1$
Let $W_i(x)=(x-x_0)(x-x_1)(x-x_2)...(x-x_{i+1})...(x-x_N)$
* The function $W_i$ is such that we do have the required roots, i.e. it equals zeros at nodes $x_0,x_1,x_2,...,x_N$ except at node $x_i$
* Degree of $W_i(x)$ is N
* However $W_i(x)$ in the form presented will not equal to unity at $x_i$
We normalize $W_i(x)$ and define the Lagrange basis functions $V_i(x)$:
$$V_i(x)=\frac{(x-x_0)(x-x_1)(x-x_2)...(x-x_{i-1})(x-x_{i+1})...(x-x_N)}{(x_i-x_0)(x_i-x_1)(x_i-x_2)...(x_i-x_{i-1})(x_i-x_{i+1})...(x_i-x_N)}$$
Now we have $V_i(x)$ such that $V_i(x_i)$ equals:
$$\begin{gather*}
V_i(x)=\frac{(x_i-x_0)(x_i-x_1)(x_i-x_2)...(x_i-x_{i-1})(1)(x_i-x_{i+1})...(x_i-x_N)}{(x_i-x_0)(x_i-x_1)(x_i-x_2)...(x_i-x_{i-1})(x_i-x_{i+1})...(x_i-x_N)} \\
\\
\to V_i(x_i)=1
\end{gather*}$$
We alos satisfy $V_i(x_j)=0$ for $i\neq j$
e.g.
$$V_1(x_2)=\frac{(x_2-x_0)(1)(x_2-x_2)(x_2-x_3)...(x_2-x_N)}{(x_1-x_0)(1)(x_1-x_2)(x_1-x_3)...(x_1-x_N)}=0$$
The general form of the interpolating function g(x) with the specified form of $V_i(x)$ is:
$$g(x)=\sum_{i=0}^{N}f_iV_i(x)$$
* The sum of polynomials of degree N is also polynomial of degree N
* g(x) is equivalent to fitting the power series and computing coefficients $a_0,...,a_N$
## Lagrange Linear Interpolation Using Basis Functions
Linear Lagrange (N=1) is the simplest form of Lagrange Interpolation:
$$\begin{gather*}
g(x)=\sum_{i=0}^{1}f_iV_i(x) \\
\to g(x)=f_0V_0(x)+f_1V_1(x)
\end{gather*}$$
where
$$V_0(x)=\frac{(x-x_1)}{(x_0-x_1)}=\frac{(x_1-x)}{(x_1-x_0)}$$
and
$$V_1(x)=\frac{(x-x_0)}{(x_1-x_0)}$$
## Example
Given the following data:
$$\begin{gather*}
x_0=2 & f_0=1.5 \\
x_1=5 & f_1=4.0
\end{gather*}$$
Find the linear interpolating function g(x)
Lagrange basis functions are:
$$\begin{gather*}
V_0(x)=\frac{x-5}{-3} \\
\\
V_1(x)=\frac{x-2}{3}
\end{gather*}$$
Interpolating function g(x) is:
$$g(x)=1.5V_0(x)+4.0V_1(x)$$
## 外部参考资料
1. [原文](https://coast.nd.edu/jjwteach/www/www/30125/pdfnotes/lecture3_6v13.pdf)